CARL FRIEDRICH
GAUSS
Johann Carl Friedrich Gauss ( 30 April 1777 – 23 February
1855) was a German mathematician and physicist who made significant
contributions to many fields, including algebra, analysis, astronomy, differential geometry, electrostatics, etc.
Sometimes referred to as the Princeps
mathematicorum (Latin for "the foremost of
mathematicians") and "the greatest mathematician since
antiquity", Gauss had an exceptional influence in many fields of
mathematics and science, and is ranked among history's most influential
mathematicians.
Early Life
Johann Carl Friedrich Gauss was born on 30
April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now
part of Lower Saxony, Germany), to poor, working-class
parents. His mother was illiterate and never recorded the date of his
birth, remembering only that he had been born on a Wednesday, eight days before
the Feast of the Ascension (which occurs 39
days after Easter). Gauss later solved this puzzle about his birth date in the
context of finding the date of Easter, deriving methods to compute the
date in both past and future years. He was christened and confirmed in
a church near the school he attended as a child.
Gauss was a child
prodigy. A contested story relates that, when he was eight, he figured out
how to add up all the numbers from 1 to 100. There
are many other anecdotes about his precocity while a toddler, and he made his
first groundbreaking mathematical discoveries while still a teenager. He
completed his magnum opus, Disquisitiones Arithmeticae, in
1798, at the age of 21—though it was not published until 1801. This work was
fundamental in consolidating number theory as a discipline and has shaped the
field to the present day.
Career and
achievements
Algebra
In his 1799 doctorate in
absentia, A new proof of the theorem that every integral rational algebraic
function of one variable can be resolved into real factors of the first or
second degree, Gauss proved the fundamental theorem of algebra which
states that every non-constant single-variable polynomial with
complex coefficients has at least one complex root. Mathematicians including Jean le Rond d'Alembert had produced
false proofs before him, and Gauss's dissertation contains a critique of
d'Alembert's work. Ironically, by today's standard, Gauss's own attempt is not
acceptable, owing to the implicit use of the Jordan curve theorem. However, he subsequently
produced three other proofs, the last one in 1849 being generally rigorous. His
attempts clarified the concept of complex numbers considerably along the way.
Gauss also made important
contributions to number theory with his 1801 book Disquisitiones Arithmeticae (Latin, Arithmetical
Investigations), which, among other things, introduced the
symbol ≡ for congruence and used it in a clean
presentation of modular arithmetic, contained the first two
proofs of the law of quadratic reciprocity, developed the theories
of binary and ternary quadratic
forms, stated the class number problem for them, and showed
that a regular heptadecagon (17-sided polygon) can be constructed with straightedge
and compass. It appears that Gauss already knew the class number formula in 1801.
In addition, he proved the
following conjectured theorems:
He also
· invented the Cooley–Tukey FFT algorithm for
calculating the discrete Fourier transforms 160
years before Cooley and Tukey
Astronomy
In the same year, Italian
astronomer Giuseppe Piazzi discovered the dwarf
planet Ceres. Piazzi could only track Ceres for
somewhat more than a month, following it for three degrees across the night
sky. Then it disappeared temporarily behind the glare of the Sun. Several
months later, when Ceres should have reappeared, Piazzi could not locate it:
the mathematical tools of the time were not able to extrapolate a position from
such a scant amount of data—three degrees represent less than 1% of the total
orbit.
Gauss, who was 24 at the
time, heard about the problem and tackled it. After three months of intense
work, he predicted a position for Ceres in December 1801—just about a year
after its first sighting—and this turned out to be accurate within a
half-degree when it was rediscovered by Franz Xaver von Zach on 31 December
at Gotha, and one day later by Heinrich Olbers in Bremen.
Gauss's
method involved determining a conic
section in space, given one focus (the Sun) and the conic's
intersection with three given lines (lines of sight from the Earth, which is
itself moving on an ellipse, to the planet) and given the time it takes the
planet to traverse the arcs determined by these lines (from which the lengths
of the arcs can be calculated by Kepler's Second Law). This
problem leads to an equation of the eighth degree, of which one solution, the
Earth's orbit, is known. The solution sought is then separated from the
remaining six based on physical conditions. In this work, Gauss used
comprehensive approximation methods which he created for that purpose.
One such method was the fast Fourier transform. While this method is
traditionally attributed to a 1965 paper by J. W.
Cooley and J. W. Tukey,[54] Gauss
developed it as a trigonometric interpolation method. His paper, Theoria
Interpolationis Methodo Nova Tractata, was only published posthumously in
Volume 3 of his collected works. This paper predates the first presentation
by Joseph Fourier on the subject in 1807.
Zach noted that "without
the intelligent work and calculations of Doctor Gauss we might not have found
Ceres again". Though Gauss had up to that point been financially supported
by his stipend from the Duke, he doubted the security of this arrangement, and
also did not believe pure mathematics to be important enough to deserve
support. Thus he sought a position in astronomy, and in 1807 was appointed
Professor of Astronomy and Director of the astronomical observatory in Göttingen, a post he held for
the remainder of his life.
The discovery of Ceres led
Gauss to his work on a theory of the motion of planetoids disturbed by large
planets, eventually published in 1809 as Theoria motus corporum
coelestium in sectionibus conicis solem ambientum (Theory of motion of
the celestial bodies moving in conic sections around the Sun). In the process,
he so streamlined the cumbersome mathematics of 18th-century orbital prediction
that his work remains a cornerstone of astronomical computation. It introduced
the Gaussian gravitational constant,
and contained an influential treatment of the method
of least squares, a procedure used in all sciences to this day to minimize
the impact of measurement error.
Gauss proved the method under
the assumption of normally distributed errors (see Gauss–Markov theorem; see also Gaussian). The
method had been described earlier by Adrien-Marie Legendre in 1805, but Gauss
claimed that he had been using it since 1794 or 1795. In the history of
statistics, this disagreement is called the "priority dispute over the discovery
of the method of least squares."
Geodetic
survey
In 1818 Gauss, putting his
calculation skills to practical use, carried out a geodetic survey of
the Kingdom of Hanover, linking up with previous
Danish surveys. To aid the survey, Gauss invented the heliotrope, an instrument that uses a
mirror to reflect sunlight over great distances, to measure positions.
Non-Euclidean
geometries
Gauss also claimed to have
discovered the possibility of non-Euclidean geometries but never
published it. This discovery was a major paradigm shift in mathematics, as it
freed mathematicians from the mistaken belief that Euclid's axioms were the
only way to make geometry consistent and non-contradictory.
Research on these geometries
led to, among other things, Einstein's
theory of general relativity, which describes the universe as non-Euclidean.
His friend Farkas Wolfgang Bolyai with whom Gauss had sworn
"brotherhood and the banner of truth" as a student, had tried in vain
for many years to prove the parallel postulate from Euclid's other axioms of
geometry.
Bolyai's son, János
Bolyai, discovered non-Euclidean geometry in 1829; his work was published
in 1832. After seeing it, Gauss wrote to Farkas Bolyai: "To praise it
would amount to praising myself. For the entire content of the work ...
coincides almost exactly with my own meditations which have occupied my mind
for the past thirty or thirty-five years."
This unproved statement put a
strain on his relationship with Bolyai who thought that Gauss was
"stealing" his idea.
Letters from Gauss years
before 1829 reveal him obscurely discussing the problem of parallel
lines. Waldo Dunnington, a biographer of Gauss, argues
in Gauss, Titan of Sciencethat Gauss was in fact in full possession
of non-Euclidean geometry long before it was published by Bolyai, but that he
refused to publish any of it because of his fear of controversy.
Theorema
Egregium
The geodetic survey of
Hanover, which required Gauss to spend summers traveling on horseback for a
decade, fueled Gauss's interest in differential geometry and topology,
fields of mathematics dealing with curves and surfaces. Among other things, he came up with
the notion of Gaussian curvature. This led in 1828 to an
important theorem, the Theorema
Egregium (remarkable theorem), establishing an important
property of the notion of curvature. Informally, the theorem says that the curvature
of a surface can be determined entirely by measuring angles and distances on
the surface.
That is, curvature does not
depend on how the surface might be embedded in
3-dimensional space or 2-dimensional space.
In 1821, he was made a
foreign member of the Royal Swedish Academy of Sciences.
Gauss was elected a Foreign Honorary Member of the American Academy of Arts and
Sciences in 1822.
Magnetism
In 1831, Gauss developed a
fruitful collaboration with the physics professor Wilhelm Weber, leading to new knowledge
in magnetism (including
finding a representation for the unit of magnetism in terms of mass, charge,
and time) and the discovery of Kirchhoff's circuit laws in
electricity. It was during this time that he formulated his namesake law.
They constructed the first electromechanical telegraph in
1833, which connected the observatory with the institute for physics in
Göttingen. Gauss ordered a magnetic observatory to
be built in the garden of the observatory, and with Weber founded the
"Magnetischer Verein" (magnetic club in German), which
supported measurements of Earth's magnetic field in many regions of the world.
He developed a method of measuring the horizontal intensity of the magnetic
field which was in use well into the second half of the 20th century, and
worked out the mathematical theory for separating the inner and outer (magnetospheric)
sources of Earth's magnetic field.
Later years
and death
Gauss remained mentally
active into his old age, even while suffering from gout and general
unhappiness. For example, at the age of 62, he taught himself
Russian.
In 1840, Gauss published his
influential Dioptrische Untersuchungen, in which he gave the first
systematic analysis on the formation of images under a paraxial approximation (Gaussian
optics). Among his results, Gauss showed that under a paraxial
approximation an optical system can be characterized by its cardinal points and he
derived the Gaussian lens formula.
In 1845, he became an
associated member of the Royal Institute of the Netherlands; when that became
the Royal Netherlands
Academy of Arts and Sciences in 1851, he joined as a foreign member.
In 1854, Gauss selected the
topic for Bernhard Riemann's Habilitationsvortrag,
"Über die Hypothesen, welche der Geometrie zu Grunde liegen"
(habilitation lecture About the hypotheses that underlie Geometry). On
the way home from Riemann's lecture, Weber reported that Gauss was full of
praise and excitement.
On 23 February 1855, Gauss
died of a heart attack in Göttingen (then Kingdom of Hanover and now Lower Saxony);
he is interred in the Albani
Cemetery there. Two people gave eulogies at his funeral: Gauss's
son-in-law Heinrich Ewald, and Wolfgang Sartorius von
Waltershausen, who was Gauss's close friend and biographer. Gauss's brain
was preserved and was studied by Rudolf
Wagner, who found its mass to be slightly above average, at
1,492 grams, and the cerebral area equal to 219,588 square millimetres
(340.362 square inches). Highly developed convolutions were also found, which
in the early 20th century were suggested as the explanation of his genius.




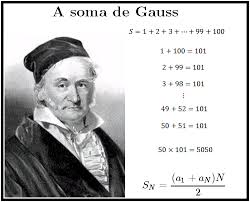







ReplyDeleteToday I was surfing on the internet & found this article I read it & it is really amazing articles on the internet on this topic thanks for sharing such an amazing article
Social Work Assignments